The gray level Size Zone Matrix (SZM) is the starting point of Thibault matrices.
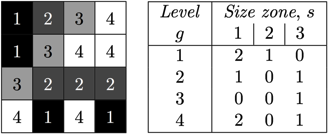
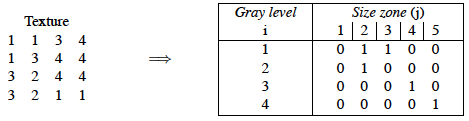
For a texture image f with N gray levels, it is denoted GSf(s, g) and provides a statistical representation by the estimation of a bivariate conditional probability density function of the image distribution values. It is calculated according to the pioneering Run Length Matrix principle: the value of the matrix GSf(s, g) is equal to the number of zones of size s and of gray level g. The resulting matrix has a fixed number of lines equal to N, the number of gray levels, and a dynamic number of columns, determined by the size of the largest zone as well as the size quantization.
The more homogeneous the texture, the wider and flatter the matrix. SZM does not required computation in several directions, contrary to RLM and co-occurrences matrix (COM). However, it has been empirically proved that the degree of gray level quantization still has an important impact on the texture classification performance. For a general application it is usually required to test several gray level quantization in order to find the optimal one with respect to a training dataset. Empirically, 32 provides often the best result.
More precisely, this matrix is particularly efficient to characterize the texture homogeneity, non periodicity or speckle like texture; it had provided betters characterizations than granulometry (or COM, RLM, etc.) for the classification of cell nuclei, dermis, road quality (bitumen condition) and some textures in PET images.
Two examples of matrix filling for textures 4x4 with four gray levels.
You can see in this paper that this method has become a standard in radiomics.
On this page is a software to fill the matrix and compute the features.
Do not hesitate to contact me if you need some explanations.
For more details about the matrix filling and features extraction, see the citations below.
Related publications:
- 1 - Texture Indexes and Gray Level Size Zone Matrix. Application to Cell Nuclei Classification, PRIP 2009.
- 2 - Shape and Texture Indexes: Application to Cell Nuclei Classification, IJPRAI 2013.
- 3 - Advanced Statistical Matrices for Texture Characterization: Application to Cell Classification, IEEE Transaction on BioMedical Engineering 2014.
- 4 - Fuzzy Statistical Matrices for Cell Classification, ArXiv 2016.
If you are interested by some old code (the most up to date being into the software above), see below.
A java source code which fills the matrix.
On this matrix, we can compute all the second-order moments of GSf(s, g) as compact texture features (take a look on links 1 to 5).
This java source code computes the indexes/features. Caution, it requires the previous java source code (see link two lines upper).
And this is an example of how use this code :
BufferedImage image = ... ; // use your reader
GlszmFeatures glszm = new GlszmFeatures() ;
glszm.Parameters(nbGrayLevel, nbSizes, FixedSize, reducer, ForbiddenValue, EightConnex, nbCPU) ;
glszm.Compute(vignette, nbCPU) ;
double[] features = glszm.Features() ;
with:
- nbGrayLevel is the number of gray level after reduction. After reduction of gray level, the matrix is more robust to noise.
- nbSizes is a coefficient to reduce the size zone. If it is equal to 1, any reduction is done. This reduction reduces the matrix width and improves slightly performances because zones with close sizes are now in the same case.
- FixedSize is a variable to know if the matrix must have a fixed size. Empirically, I have never obtained better results with a fixed size, so my advice is to always use this parameter as « false ».
- reducer reduces the number of gray level. Use this one.
- ForbiddenValue The value to not take into account during computations. If it is equal to a negative value, the entire texture is process. Caution, that can depend on the class which labels connected component.
- EightConnex Is the labeling realized with 8-connexity?
- nbCPU is the number of thread to use for processing. As the connected component labeling is not parallelized (not in my library, but maybe algorithms exists), this parameter value doesn’t matter.
Here is a complete example.