1 - Vous disposez d'une balance classique à deux plateaux et neufs boules d'apparences identiques dont l'une d'elles est un peu plus lourde.
Comment retrouver la boule plus lourde en 2 pesées ?
2 - Comment relier ces neuf points en quatre traits sans lever le stylo ?

3 - Qu'ont en commun les six chiffres suivant ?
0 2 5 7 8 9
4 - Dans la jungle un père et ses deux fils doivent traverser une rivière.
Sachant que la barque ne peut contenir que 100 kg, que le père pèse 100 kg et que ses deux fils pèsent chacun 50 kg, comment feront t'ils pour passer de l'autre coté de la rivière?
5 - Comment faire 4 triangles avec 6 allumettes? (sans les casser)
6 - Comment faire 6 triangles équilatéraux avec 6 allumettes? (sans les casser)
7 - Un escargot est au fond d'un puits. Le puits a trente mètres de profondeur.
L'escargot avance de trois mètres en une journée.
Pendant la nuit il glisse deux mètres vers le bas du puits.
Question : Combien de jours prendra-t-il pour sortir du puits ?
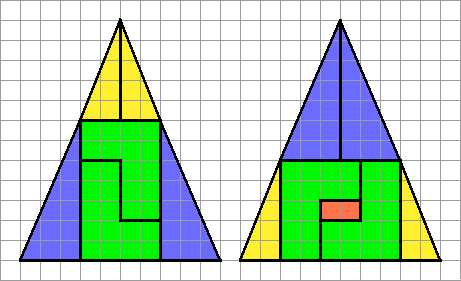
8 - Le triangle de Curry.
Les parties de la première figure ont été regroupées différemment pour former la seconde, à la différence qu'il faut ajouter à ce dernier deux petits carrés.
Comment expliquer la présence de ce rectangle rouge ?
9 - Comment couper un gâteau en huit morceaux en trois coups de couteau ?
10 - Comment obtenir un carré en ne bougeant qu'une seule allumette ?
11 - La disparition des nains.
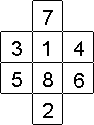
12 - On doit placer chacun des chiffres de 1 à 8 de façon à ce qu'aucun ne soit en contact ni par un côté ni par une diagonale avec le chiffre qui le précède ou celui qui le suit.

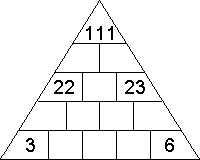
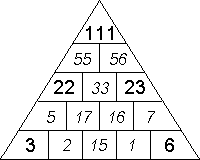
13 - Compléter ce triangle de manière à ce que le nombre inscrit dans chaque case soit égal à la somme des deux nombres inscrits dans les deux cases juste en dessous celle-ci.
14 - Combien y a-t-il, au total, de carrés dans la figure ci-dessous ?

15 - Un problème classique pour les joueurs d'échec.
Comment disposer huit reines sur un échiquier de façon à ce qu'aucune d'entre elles ne soit mise en échec par une autre ?
16 - Un problème facile et classique. Trouver la suite :
1
11
21
1211
111221
312211
17 - Quelle est la valeur du produit suivant ?
(x-a)(x-b)(x-c)(x-d)... (x-y)(x-z)
en tout 26 couples de parenthèses ; avec a, b ... z des nombres quelconques (réels ou complexes).
18 - A quelle époque de l'humanité cette égalité a-t-elle été vérifiée ?
31 oct. = 25 déc.
19 - Vous êtes sur une île avec un loup, une chèvre et un chou ;
vous devez au moyen d'une barque les emmener tous trois sur une autre île.
La barque étant très petite, vous ne pouvez malheureusement n'en transporter qu'un à la fois.
Comment doivent s'organiser les traversées afin qu'aucun ne se fasse dévorer par un autre ?
20 - Deux pères et deux fils sont assis autour d'une table ; sur cette table se trouvent quatre oranges, chacun en prend une ; suite à cela, il reste une orange sur la table.
Comment est ce possible ?
21 - Un émir mourant fait venir auprès de lui ses deux fils.
Il leur dit : Vous voyez à l'horizon le minaret de la ville voisine ?
Et bien, celui d'entre vous dont le cheval arrivera en dernier au pied de ce minaret héritera de mon immense fortune.
Les deux fils se précipitent vers l'écurie et partent au triple galop vers le minaret.
Pourquoi se pressent-ils ainsi ?
22 -

23 - Trois amis font un concours. Le gagnant partira pour un voyage offert par les deux perdants. L'un d'entre eux est aveugle, un autre borgne, et le dernier bien voyant.
Le concours est simple : 4 balles, 3 noires et 1 blanche, sont dans un sac non transparent. Chacun prend une balle et la met sur sa tête sans la regarder.
Le premier qui devine la couleur de sa balle du premier coup part en voyage.
Si la réponse est mauvaise, il finance le voyage aux 2 autres.
Au bout d'une demi-heure de silence, l'aveugle s'exclame à la grande surprise de ses deux compagnons : "Je sais de quelle couleur est ma balle !"
De quelle couleur est sa balle ?
Comment l'a-t-il su ?
24 - Vous êtes face à 2 portes, l'une donne sur l'enfer et l'autre sur le paradis. Vous ne savez pas laquelle mène au paradis, et laquelle à l'enfer.
Juste à côté de ces portes, sont présentes deux personnes : l'une est un menteur, l'autre dit toujours la vérité.
Vous ne pouvez poser qu'une seule question pour savoir quelle porte prendre.
Quelle est cette question ?
Indices :
1 - Décomposez les boules en trois groupes.
2 - On peut déborder du cadre, passer deux fois par le même point et croiser les traits.
3 - Le chiffre quatre leurs est commun, pourquoi ? Il n'y a rien de mathématique dans ce problème.
4 - La barque doit faire deux aller/retour puis un aller.
5 - Ne pas se limiter au plan.
6 - On peut les superposer.
7 - Attention au dernier jour.
8 - Observez les cotés des triangles.
9 - Coupez dans les trois plans.
10 - Le mot "carré" à plusieurs sens en mathématique.
11 -
12 - Deux chiffres sont particuliers, il faut les placer au milieu.
13 -
14 - Compter tous les carrés de tailles 1, 2, ... 16
15 - Les reines peuvent bouger dans toutes directions et d'autant de case qu'elles le souhaite, donc il faut les mettre une par ligne et par colonne.
16 - Comptez à haute voix le contenu des lignes.
17 - Imaginez tous les couples.
18 - oct n'est pas forcément octobre.
19 - Il faut faire deux allé/retour puis un allé.
20 - Pensez à tous les membres d'une famille.
21 - A cheval volé on ne regarde pas les dents.
22 - Attention à la réponse.
23 - Se mettre à la place des autres.
24 - Ne pas poser une question directe.
Solutions :
1 - On commence par séparer les boules en trois groupes de trois boules.
On place sur la balance deux des trois groupes de trois boules, il y a alors deux possibilités :
-> La balance ne penche d'aucun coté, cela implique que la boule plus lourde est dans le troisième groupe qui n'est pas pesé.
-> La balance penche d'un coté, cela implique que la boule recherchée est du coté qui penche.
On sait maintenant dans quel groupe est la boule recherchée.
On place deux des boules du dernier groupe sur la balance et là, encore deux possibilités :
-> La balance ne penche pas, donc la boule recherchée est celle qui n'a pas été pesée.
-> La balance penche, elle indique qu'elle est la boule recherchée.
2 -

3 - Les chiffres zéro, deux, cinq, sept, huit et neuf s'écrivent tous avec quatre lettres.
4 - En premier ce sont les deux fils qui vont de l'autre coté, un restera sur la rive et l'autre repart rejoindre son père.
Il laisse son père monter sur la barque et reste de l'autre coté.
Le père rejoint alors son fils qui était déjà de l'autre coté de la rivière.
Le frère déjà passé rejoint son frère le laisse monter sur la barque et ne descend pas de la barque et ils rejoignent le père.
Ainsi tous les 3 arriverons de l'autre coté.
5 - Construire un tétraèdre.
6 - Construire deux triangles et superposer les triangles afin de construire une étoile de David. Cela formera six triangles équilatéraux.
7 - 28 jours.
8 - Ce ne sont pas des triangles, regardez les schémas suivant pour vous en convaincre.
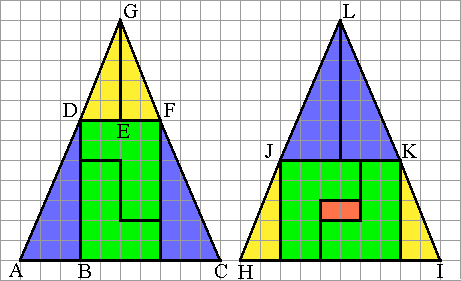
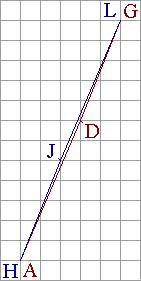
9 - Il faut couper sur la longueur, la largeur et la... hauteur (horizontalement).
10 - Au sens arithmétique, quatre est la carré de deux.
12 - Les chiffres 1 et 8 ont un seul voisin, il faut les placer au milieu pour minimiser les risques de suite.
Voilà une solution, on peut bien entendu construire les autres par symétrie.
13 -
14 - 30 => 16 de taille 1x1, 9 de taille 2x2, 4 de taille 3x3 et 1 de taille 4x4
15 - Il y a beaucoup d'autres solutions. Ce problème se généralise pour des échiquier de taille NxN

16 - Regardons ligne par ligne :
Première ligne : 1, à haute voix on compte un un => 11
Deuxième ligne : 11, deux un => 21
Troisième ligne : 21, un deux et un un => 1211
...
17 - 0, car il y a le couple x-x.
18 - A n'importe qu'elle époque : 31 en octal vaut toujours 25 en décimal.
19 - Comme il ne faut jamais laisser sur une même île deux éléments qui pourraient se nuire, on commence par faire traverser la chèvre car elle est l'élément médiant (entre le loup et le chou). Puis on revient chercher un des deux autres ( par exemple le chou ) que l'on fait traverser. Une fois sur la seconde île, on ne peut laisser en présence la chèvre et le chou ; on fait donc à nouveau traverser la chèvre qui retourne ainsi sur la première île. Puis on transporte le loup afin d'éviter à la chèvre de se faire croquer. Sur la seconde île on laisse ensemble le chou et le loup, ce qui sera sans consequences ; il ne nous reste plus qu'à aller sur la première île chercher la chèvre.
20 - Il y a effectivement trois personnes à table. Le fils, le père et le grand-père. Le père jouant à la fois le role de père et de fils.
21 - Chacun a pris le cheval de l'autre.
22 - Trois ne peut pas convenir, car il contient un R. Quatre convient alors :

23 - L'aveugle se doutait que, puisque le bien-voyant voit, il a dû voir deux balles noires sur la tête de ses deux compagnons. C'est pour cela que le bien-voyant n'a pas pu savoir si sa balle était noire ou blanche.
Idem pour le borgne qui voit quand-même d'un oeil.
L'aveugle en a déduit que sa balle était noire !
24 - Il faut demander : "Quelle porte me désignera l'autre personne si je lui demande quelle est la porte du paradis ?".
Lorsque je la pose au juste, il me désignera la porte de l'enfer (en effet, le menteur m'aurait montré celle-ci). Lorsque je la pose au menteur, il me désignera aussi la porte de l'enfer (en effet, le juste m'aurait montré la porte du paradis donc le menteur me montrera l'autre).
Il me suffit de prendre la porte qu'aucun n'aura désignée.